“转化思想”与分数应用题教学

　自课改以来，“应用题”好像已不常被专家、教师所提及，教材也不单设纯粹的应用题章节。但是“综合运用所学知识解决简单的实际问题”永远是小学数学学习的重要内容与目标。

　　

　　笔者一直致力于分数应用题教学的研究与实践，结合本人课题研究，欲以“转化”这一数学思想方法为切入点，谈点个人对分数应用题教学的实践与思考，以期与同行商榷。

　　

　　一、分数应用题内容特点及教学现状简析

　　

　　1．分数应用题内容特点

　　

　　从整体分析，单纯研究量的分数应用题与第一、二学段的整数应用题只是数字形式不同，故其不在本文所谈之列。

　　

　　（图一）

　　

　　较一、二学段应用题而言，分数应用题因增加了分率与分率关系、数量与分率关系。所以内容抽象性强、变化多，加之学习时间跨度长，因此成为教、学的

　　

　　难点。研究过程中通过对知识点梳理，我们建立了其知识网络（图一）。从图中分析：分数应用题学习以除法为基础，以分数意义、分数乘法意义为核心概念，是与后续内容“比”融为一体的。而一般分数应用题可分为三大种九小类。

　　

　　2．教学现状

　　

　　模式化：即把分数应用题分为求分率、求对应量、求单位“1”三类，再按一定步骤、固定模式进行解答（如本刊14年1-2期徐启春、刘焱撰文所述）。这种方法学生可能正确率较高但对内容不理解，不利于学生数学学习能力提升。

　　

　　板块化：教学结合分数意义、分数乘法意义，但把分数应用题按解答方法进行严格分类教学，重视不同题型特征总结。这种方法加深了学生对分数应用题的理解，但缺乏对知识的整体把握，不利于学生形成较为完善的认知结构。

　　

　　二、运用转化思想的价值探析

　　

　　概括讲，数学教学中运用转化的目的就是为达到求同、求简、求通。那么在分数应用题教学中运用转化思想有何价值？

　　

　　1．分率转化，感悟分数应用题数量关系的基石。

　　

　　“分率”即表示两个量或率间的关系，常以倍、分数、百分数、比等形式出现。

　　

　　较低年级学习的应用题而言，分数应用题数量关系除了具体量间的关系外，增加了具体量所对应的分率间的关系。如“学校有学生900人，男生人数是女生的。男、女生各有多少人？”，该题具体量间的关系是“男生人数＋女生人数＝全校总人数”，但要解决问题学生必须先清楚这三个量所对应的份数与相应标准量的关系（即分率），而标准量的确定又需据题意及解题思路灵活变化，这是分数应用题让学生感觉学习困难的主要原因。

　　

　　解决该困难不可能一撮而就，需教师在相关内容教学时有意识地指导、训练。如分数意义学习时：如何理解“看了一本书的”，除了知道“把一本书的页数平均分成5份，看了的页数相当于这样的2份”外，教师应指导学生思考还能知道什么？①还剩这本书的；②已看是剩下的，剩下是已看的（1.5倍）；③全书是已看的，全书是剩下的。如百分数意义学习时：如何理解“九月份用水比八月份节约20%”，① 九月份比八月份节约用水量是八月份的20%；②九月份用水量相当于八月份的80%（），八月份用水量相当于九月份的（125%）；③八月份用水量比九月份多25%。学习“比”时更可把倍、分率、比等进行综合转化。

　　

　　整体把握教材，运用转化帮助学生联系除法、倍、分数与比，帮助学生理解同一个量的对应分率会随标准量的变化而变化，学生就能感悟分数应用题的数量关系。这样做，你一定会惊讶学生在学习分数应用题时的表现。

　　

　　2．题型转化，掌握分数应用题解题方法的核心。

　　

　　分率转化的体验与训练为学生解决图一中的A类题奠定了扎实基础。现就阐述运用转化思想解决B、C类题。

　　

　　B、C类题的解决方法可统一到分数乘法的意义上，即根据求一个数的几分之几是多少用乘法。如解决“水果店运进苹果600㎏，运进橘子的重量是苹果的。水果店运进橘子多少㎏？”时，指导学生结合题意及分数乘法意义理解解题思路、列式依据。而下表题目（通常称分数除法应用题）的解决则把解题思路通过转化统一到分数乘法意义中。

　　

　　

　　

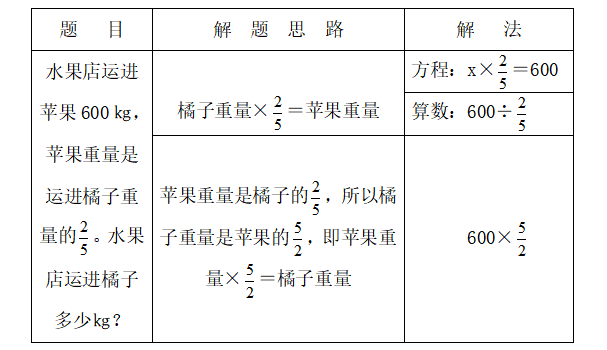
　　对于稍复杂的B、C类题教学，亦可在上述基础上通过转化求同、求简。

　　

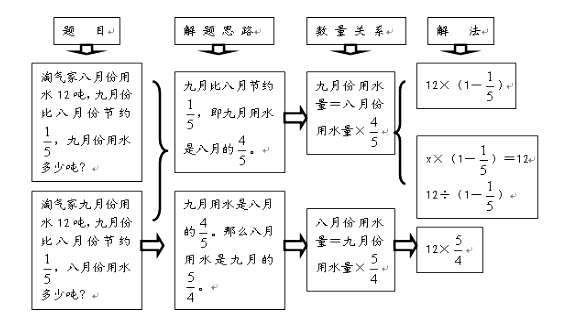
　　按这种方法组织教学就不再把分数应用题分为乘、除法应用题，也就不需学生记忆求“单位1”还是“对应量”的模式化方法，且还可把两步应用题转化为一步。这样的教学利于学生从整体上建立对分数应用题的认知结构，掌握分数应用题的一般解题方法。当然前提是学生理解分率转化并能较熟练运用。

　　

　　3．综合转化，形成分数应用题解决策略的灵魂

　　

　　分数应用题变化丰富，解决时所需知识综合性强，因此解决思路复杂、策略多样。欲使学生形成分数应用题解决策略，学习过程需引导学生不断思考、比较、转化。

　　

　　例1：行完AB两地奇思需要4时，妙想需要5时。如果他俩分别同时从A、B两地相向而行，相遇时奇思比妙想多行12千米。A、B两地相距多少千米？该题综合了行程问题与分数应用题相关知识点，特征为缺少表示路程（速度）的具体量，关键是找出“相同时间（相遇时）内奇思比妙想多行的12千米是A、B全程的几分之几”。解题思路为：1）把奇思、妙想的速度转化为分率表示即、；2）根据相遇问题数量关系求出相遇时间1÷（＋）＝（时）；3）根据追及问题数量关系得出相遇时奇思比妙想多行的12千米就是全程的（－）×＝；4）根据分数乘法意义求全程12÷＝108（千米）。

　　

　　上题的解决过程是行程问题与分数应用题不断相互转化的过程，解题时既需要学生把分数应用题的思考方式用到行程问题中，又要把行程问题的数量关系转化成分数应用题的形式表示。

　　

　　例2：某旅游景点为招揽游客，决定把门票降价30元，结果游客数量增加了，门票收入增加了。该景点门票原价多少元？学生解决此类问题往往觉得无从下手。该题难点为游客数量与门票收入无具体量，而有具体量的门票单价却不知降价前后的关系。解决此题除了假设游客具体数量外可用列表法引导学生分析：本题基本数量关系为“单价×数量＝总价”，有降价前后两层关系，根据需

　　

　　

　　

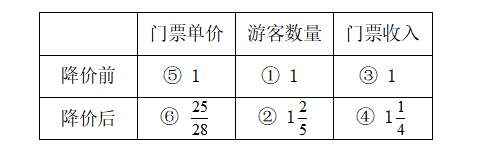
　　要设计成表格。1）据游客数量增加填写表格①、②处；2）据门票收入增加填写表格③、④处；3）据单价×数量＝总价分别计算表格⑤、⑥处；4）据表格⑤、⑥处得出30元就是门票原价的，从而求出门票原价。

　　

　　例2的解决过程可以理解成价格关系与分数应用题不断转化的过程。首先根据题意把游客数量与门票收入转化成分率，这样便于学生理解降价前后它们之间的关系。其次把价格关系转化为纯分率表示（学生原来以具体量表示为主），从而求得降价前后门票单价的分率；最后根据降价前后门票单价的关系及相差的30元解决问题。

　　

　　分数应用题的特点之一是从研究量转变成研究关系。以上两例学习过程意在使学生把以往学习的数量关系、解决问题的方法经验通过转化统一到分数应用题的解题策略中，达到丰富解题策略，提升学习能力的目的。

　　

　　分数应用题学习过程需要落实的数学思想方法很多，如对应思想、数形结合思想、函数思想……数学思想方法是数学的灵魂，要想学好数学、用好数学，就要引导学生深入到数学的“灵魂深处”。